
Figure 1: Distance from MH light source versus light intensity (measured and calculated).
To determine the relationship, if any, between light intensity and distance from a lamp. It is obvious that light intensity drops as you move further away from the light source. Theoretically, with all other factors being equal, the inverse square rule should dominate the change in intensity.
The inverse square rule states that if the intensity at point X from a single point light source is A, the intensity at X+Y will be A/Y^2.
A lamp was positioned on a bench top such that it was pointing in a direction parallel to the top of the bench. Light readings were taken at various distances from the light source and recorded.
The lamp used was a 150W Metal Halide light, fitted with a 150W 10000K double-ended lamp (BLV 221301). The lamp was around 12 months old.
A second test was performed using normal output fluorescent lighting. A new 30W Sylvania Aquastar was fitted to simple light fitting.
The meter used was a Basic Quantum Meter with Electric Light Calibration made by Apogee Instruments. The meter measures Photosynthetic Photon Flux in µE m-2s-1 (microeinsteins per square metre per second). A microeinstein is equivalent to a micromole of photons. The meter responds to light in the range 400-650nm. It underestimates light in the range 400-500nm (blue light) and overestimates light in the range 550-650nm (yellow and orange light). It is rated at an accuracy of +/-3%.
The bench top was covered with a grey blanket to reduce reflection.
Measurements for the Metal Halide lamp were taken from the outside of the UV filter on the fixture. From the outside of the UV filter to the outside of the outer lamp envelope is 1cm. The inner lamp envelope is a further 0.4cm from the outer envelope. The inner and outer envelopes are approximately 1.5cm and 2.3cm in diameter, respectively.
The lamp was fired at least 5 minutes before the tests begun, and the first reading was taken after the meter read a "constant" value for at least one minute. At close distances to the light source, the light output is very high and the meter records variations of up to 2 µE m-2 s-1.
Measurements for the Fluorescent lamp were taken from the centre of the tube and 20cm from the centre.
Table 1: Meter readings from the MH lamp at different distances from the UV Filter
|
Distance from UV filter |
Reading 1 |
Reading 2 |
Reading 3 |
Average PAR |
|
10 |
1433 |
1410 |
1411 |
1418 |
|
15 |
801 |
802 |
799 |
801 |
|
20 |
499 |
497 |
501 |
499 |
|
25 |
249 |
349 |
338 |
312 |
|
30 |
249 |
250 |
249 |
249 |
|
35 |
190 |
190 |
190 |
190 |
|
40 |
149 |
149 |
148 |
149 |
|
50 |
100 |
99 |
100 |
100 |
|
60 |
72 |
71 |
72 |
72 |
|
70 |
59 |
53 |
53 |
55 |
|
80 |
42 |
41 |
41 |
41 |
|
90 |
33 |
33 |
32 |
33 |
|
100 |
28 |
27 |
28 |
28 |
|
110 |
22 |
22 |
22 |
22 |
|
120 |
19 |
19 |
19 |
19 |
Table 2: Light intensities for the MH lamp at the corrected distances from the light source. As the measurements were taken from the outside of the UV filter, 2.3cm was added to give the distance from the centre of the lamp.
|
Distance from light (cm) |
Average |
|
12.15 |
1418 |
|
17.15 |
801 |
|
22.15 |
499 |
|
27.15 |
312 |
|
32.15 |
249 |
|
37.15 |
190 |
|
42.15 |
149 |
|
52.15 |
100 |
|
62.15 |
72 |
|
72.15 |
55 |
|
82.15 |
41 |
|
92.15 |
33 |
|
102.15 |
28 |
|
112.15 |
22 |
|
122.15 |
19 |
Table 3: Meter readings for the centre of the fluorescent tube. Distances are measured from the tube.
Distance from light (cm)
Reading 1 Reading 2 Reading 3 Average 10
108
102
101
104
15
78
79
79
79
20
57
58
58
58
25
49
49
49
49
30
37
37
37
37
35
31
31
30
31
40
28
28
29
28
50
19
19
19
19
60
19
19
19
19
70
17
17
17
17
80
9
9
9
9
90
7
7
7
7
100
8
8
8
8
110
9
9
9
9
120
9
9
9
9
(µE m-2 s-1)
(µE m-2 s-1)
(µE m-2 s-1)
(µE m-2 s-1)
Table 4: Meter readings for 20cm from the centre of the fluorescent tube.
|
Distance from light (cm) |
Reading 1 (µE m-2 s-1) |
Reading 2 (µE m-2 s-1) |
Reading 3 (µE m-2 s-1) |
Average (µE m-2 s-1) |
|
10 |
108 |
113 |
111 |
111 |
|
15 |
77 |
78 |
78 |
78 |
|
20 |
58 |
58 |
59 |
58 |
|
25 |
43 |
43 |
47 |
44 |
|
30 |
39 |
39 |
33 |
37 |
|
35 |
28 |
28 |
27 |
28 |
|
40 |
23 |
23 |
22 |
23 |
|
50 |
17 |
17 |
18 |
17 |
|
60 |
13 |
13 |
13 |
13 |
|
70 |
10 |
10 |
10 |
10 |
|
80 |
8 |
8 |
8 |
8 |
|
90 |
7 |
8 |
7 |
7 |
|
100 |
8 |
9 |
8 |
8 |
|
110 |
9 |
9 |
9 |
9 |
|
120 |
9 |
9 |
9 |
9 |
Table 5: Average readings for light intensity from the MH lamp compared to expected values using inverse square rule. All subsequent values are calculated from the from the first value using the following formula In=I1/((D1/Dn)2) where In is the calculated intensity at distance Dn, I1 is the first intensity, D1 is the first distance and Dn is the nth distance.
|
Distance from light (cm) |
Average PAR |
Calculated PAR |
|
12.15 |
1418 |
1418 |
|
17.15 |
801 |
712 |
|
22.15 |
499 |
480 |
|
27.15 |
312 |
319 |
|
32.15 |
249 |
228 |
|
37.15 |
190 |
171 |
|
42.15 |
149 |
133 |
|
52.15 |
100 |
87 |
|
62.15 |
72 |
61 |
|
72.15 |
55 |
45 |
|
82.15 |
41 |
35 |
|
92.15 |
33 |
28 |
|
102.15 |
28 |
23 |
|
112.15 |
22 |
19 |
|
122.15 |
19 |
16 |

Figure 1: Distance from MH light source versus light intensity (measured and calculated).
Figure 1 shows that at least in air, drop-off in light intensity with distance closely follows expected intensities based on the inverse square rule.
Table 6: Average readings for light intensity of the fluorescent lamp for both centre and 20cm from centre compared to expected values using inverse square rule. All subsequent values are calculated from the from the first value using the following formula In=I1/((D1/Dn)2) where In is the calculated intensity at distance Dn, I1 is the first intensity, D1 is the first distance and Dn is the nth distance.
Distance from light (cm) |
Average PAR @ centre (µE m-2s-1) |
Calculated PAR |
Average PAR |
Calculated PAR |
|
10 |
104 |
104 |
111 |
111 |
|
15 |
79 |
46 |
78 |
49 |
|
20 |
58 |
26 |
58 |
28 |
|
25 |
49 |
17 |
44 |
18 |
|
30 |
37 |
12 |
37 |
12 |
|
35 |
31 |
8 |
28 |
9 |
|
40 |
28 |
6 |
23 |
7 |
|
50 |
19 |
4 |
17 |
4 |
|
60 |
19 |
3 |
13 |
3 |
|
70 |
17 |
2 |
10 |
2 |
|
80 |
9 |
2 |
8 |
2 |
|
90 |
7 |
1 |
7 |
1 |
|
100 |
8 |
1 |
8 |
1 |
|
110 |
9 |
1 |
9 |
1 |
|
120 |
9 |
1 |
9 |
1 |

Figure 2: Distance from fluorescent light source versus light intensity (measured and calculated).
As fluorescent lamps are not a single point light source, light drop-off with distance does not closely follow the inverse square rule as Figure 2 shows. While the basic principle of the inverse square rule is followed, light from all points along the tube mix.
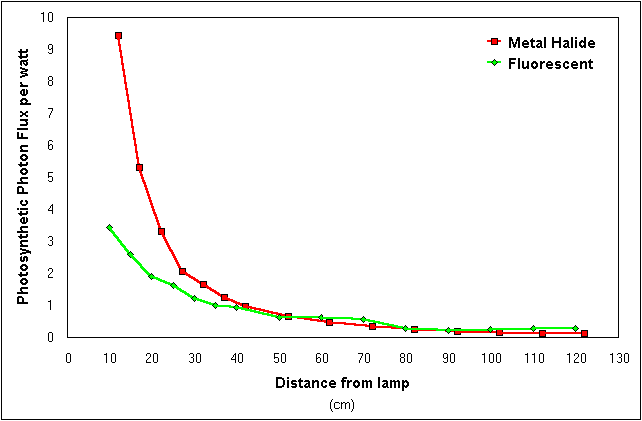
Figure 3: A comparison of Metal Halide to Fluorescent lamps. Light intensity has been divided by the rated wattage of the lamps.
Figure 3 shows that Metal Halide lights deliver more light per watt directly under the centre of the lamp than fluorescent lamps. Note that the light intensity of Metal Halide will drop off more rapidly than fluorescent lamps the further you move away from the centre.
Notes:
There are a number or areas where the measured results could be slightly inaccurate:
Last updated: October 8, 2000